Unsupervised Learning
Overview
Teaching: 45 min
Exercises: 15 minQuestions
What is principal component analysis (PCA)?
How can I perform PCA in R?
What is clustering?
Objectives
Know the difference between supervised and unsupervised learning.
Learn the advantages of doing dimensionality reduction on a dataset.
Know the basics of clustering.
Perform the k-means algorithm in R.
Learn how to read a cross table.
Unsupervised Learning I: dimensionality reduction
Machine learning is the science and art of giving computers the ability to learn to make decisions from data without being explicitly programmed.
Unsupervised learning, in essence, is the machine learning task of uncovering hidden patterns and structures from unlabeled data. For example, a business may wish to group its customers into distinct categories based on their purchasing behavior without knowing in advance what these categories maybe. This is known as clustering, one branch of unsupervised learning.
Aside: Supervised learning, which we’ll get to soon enough, is the branch of machine learning that involves predicting labels, such as whether a tumour will be benign or malignant.
Another form of unsupervised learning, is dimensionality reduction: in the breast cancer dataset, for example, there are too many features to keep track of. What if we could reduce the number of features yet still keep much of the information?
Discussion
Look at features X3 and X5. Do you think we could reduce them to one feature and keep much of the information?
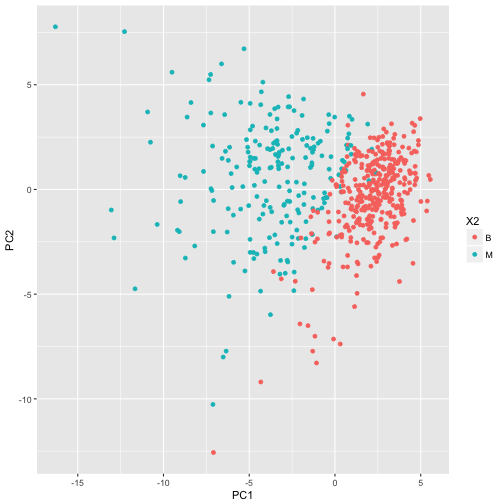
Principal component analysis will extract the features with the largest variance. Here let’s take the first two principal components and plot them, coloured by tumour diagnosis.
# PCA on data
ppv_pca <- preProcess(df, method = c("center", "scale", "pca"))
df_pc <- predict(ppv_pca, df)
# Plot 1st 2 principal components
ggplot(df_pc, aes(x = PC1, y = PC2, colour = X2)) + geom_point()
Note
What PCA essentially does is the following:
- The first step of PCA is to decorrelate your data and this corresponds to a linear transformation of the vector space your data lie in;
- The second step is the actual dimension reduction; what is really happening is that your decorrelation step (the first step above) transforms the features into new and uncorrelated features; this second step then chooses the features that contain most of the information about the data (you’ll formalize this soon enough).
You can essentially think about PCA as a form of compression. You can read more about PCA here.
Unsupervised Learning II: clustering
One popular technique in unsupervised learning is clustering. Essentially, this is the task of grouping your data points, based on something about them, such as closeness in space. What you’re going to do is group the tumour data points into two clusters using an algorithm called k-means, which aims to cluster the data in order to minimize the variances of the clusters.
Cluster your data points using k-means and then we’ll compare the results to the actual labels that we know:
# k-means
km.out <- kmeans(df[,2:10], centers=2, nstart=20)
summary(km.out)
Length Class Mode
cluster 569 -none- numeric
centers 18 -none- numeric
totss 1 -none- numeric
withinss 2 -none- numeric
tot.withinss 1 -none- numeric
betweenss 1 -none- numeric
size 2 -none- numeric
iter 1 -none- numeric
ifault 1 -none- numeric
km.out$cluster
[1] 2 2 2 1 2 1 2 1 1 1 1 1 2 1 1 1 1 1 2 1 1 1 1 2 2 2 1 2 1 2 2 1 2 2 1
[36] 2 1 1 1 1 1 1 2 1 1 2 1 1 1 1 1 1 1 2 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1
[71] 2 1 2 1 1 1 1 2 2 1 1 1 2 2 1 2 1 2 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1
[106] 1 1 1 2 1 1 1 1 1 1 1 1 1 1 2 1 2 2 1 1 1 1 2 1 2 1 1 1 1 2 1 1 1 1 1
[141] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 1 1 1 2 2 1 2 1 1 2 2 1 1 1 1 1 1
[176] 1 1 1 1 1 2 2 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 2 2 1 1 2 2 1 1 1 1 2 1 1
[211] 2 1 2 2 1 1 1 1 2 2 1 1 1 1 1 1 1 1 1 1 2 1 1 2 1 1 2 2 1 2 1 1 1 1 2
[246] 1 1 1 1 1 2 1 2 2 2 1 2 1 1 1 2 2 2 1 2 2 1 1 1 1 1 1 2 1 2 1 1 2 1 1
[281] 2 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 2 1 1 1 1 1 1 1 1 1 1 1 1
[316] 1 1 2 1 1 1 2 1 2 1 1 1 1 1 1 1 1 1 1 1 2 1 2 1 2 1 1 1 2 1 1 1 1 1 1
[351] 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 2 2 1 2 2 1 1 2 2 1 1 1 1 1 1 1 1 1 1 1
[386] 1 1 1 1 2 1 1 1 2 1 1 1 1 1 1 2 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1
[421] 1 1 1 1 1 1 1 1 1 1 1 1 2 2 1 1 1 1 1 1 1 2 1 1 2 1 2 1 1 2 1 2 1 1 1
[456] 1 1 1 1 1 2 2 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 2
[491] 1 2 2 1 1 1 1 1 2 2 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 2 2 1 1 1 2 1 1 1
[526] 1 1 1 1 1 1 1 1 2 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
[561] 1 1 1 2 2 2 2 2 1
Now that you have a cluster for each tumour (clusters 1 and 2), you can see how well they coincide with the labels that you know. To do this you’ll use a cool method called cross-tabulation: a cross-tab is a table that allows you to read off how many data points in clusters 1 and 2 were actually benign or malignant respectively.
Let’s do it:
# Cross-tab of clustering & known labels
CrossTable(df$X2, km.out$cluster)
Cell Contents
|-------------------------|
| N |
| Chi-square contribution |
| N / Row Total |
| N / Col Total |
| N / Table Total |
|-------------------------|
Total Observations in Table: 569
| km.out$cluster
df$X2 | 1 | 2 | Row Total |
-------------|-----------|-----------|-----------|
B | 355 | 2 | 357 |
| 20.579 | 73.851 | |
| 0.994 | 0.006 | 0.627 |
| 0.798 | 0.016 | |
| 0.624 | 0.004 | |
-------------|-----------|-----------|-----------|
M | 90 | 122 | 212 |
| 34.654 | 124.362 | |
| 0.425 | 0.575 | 0.373 |
| 0.202 | 0.984 | |
| 0.158 | 0.214 | |
-------------|-----------|-----------|-----------|
Column Total | 445 | 124 | 569 |
| 0.782 | 0.218 | |
-------------|-----------|-----------|-----------|
Discussion
How well did the k-means do at clustering the tumour data?
Key Points
Supervised and unsupervised learning are different machine learning techniques that are used for different purposes.
PCA can help simplify data analysis.
Clustering may reveal hidden patterns or groupings in the data.
A cross table is a tool that allows us to measure the performance of an algorithm.